Stationkeeping in Mars orbit

The title of a paper recently published in Planetary and Space Science caught my eye: "Optimal longitudes determination for the station keeping of areostationary satellites." It had never occurred to me to wonder what the orbit of a geostationary spacecraft at Mars would be like, so I asked the author (Juan Silva) for a copy of his article. One thought-provoking conclusion: it takes a lot more work to maintain a stationary orbit at an arbitrary longitude at Mars than it does at Earth.

To back up a little bit, let's talk about geostationary orbits. Most of the spacecraft that we have at Earth are in relatively low orbits. The closer you are to the thing you're orbiting, the faster you have to go to stay in orbit. Consequently most of our satellites have orbits that are much less than an Earth day long; most of them orbit Earth with periods between one and two hours.

The farther you are from the surface, the lower your orbital speed. At a certain altitude -- which, for Earth, is 35,786 kilometers (corresponding to an orbital radius of 42,155 kilometers) -- your orbital period exactly balances Earth's rotation rate. As you travel around Earth, the planet rotates underneath you, and if your orbit is circular, the net result is that you appear to be stationary, in longitude anyway. If your orbit is in the plane of Earth's equator, then you appear to be stationary in both longitude and latitude -- you're parked above that spot on Earth's equator. This is a geostationary orbit.

What is a geostationary orbit like at Mars? I have to pause here for a brief discussion of semantics. The authors of this paper discuss "areostationary" for Mars orbits as opposed to "geostationary" for Earth, and Wikipedia uses the same convention, but I'm not a big fan of this sort of nomenclatural hair-splitting. You'd have to talk about "hermestationary" for Mercury, "cronostationary" for Saturn, "selenostationary" for the Moon, and so on. It gets tiresome. And while a very few people use "areology" to name the study of rocks on Mars and "selenology" to talk about rocks on the Moon, nearly everybody calls it all "geology" and a person who studies all that stuff a "planetary geologist." So I'm going to stick with calling it a "Martian geostationary orbit."

Mars is considerably less massive than Earth (it has about 11% of Earth's mass) but rotates at about the same angular rate, so a stationary orbit at Mars will be smaller than one at Earth. The Martian geostationary orbit altitude is only 13,634 kilometers (so an orbital radius of 20,428 kilometers, or about 3,000 kilometers inside the orbit of Deimos). Another way of looking at it: the Martian geostationary orbital radius is about 6 Mars radii (or an altitude of 5 Mars radii above the surface); the Earth geostationary orbital radius is very similar at about 6.6 Earth radii (or an altitude of 5.6 Earth radii above the surface).

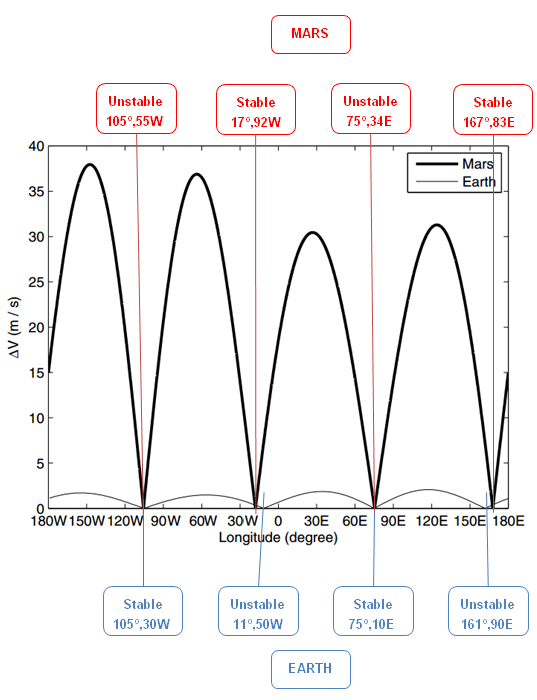
And that would be the end of the story if the planets were spherical and homogeneous and there were no other perturbing effects. But of course the real world isn't as simple as that. At Earth, the major effects on satellites trying to stay in one position are the presence of the Moon and Earth's polar flattening. These combine to tilt the plane of the satellite's orbit. Also, Earth's nonspherical shape -- the lumps and bumps that make its equator noncircular -- causes the satellite to migrate in longitude over time. There are two stable points (at 75.3E and 104.7W, corresponding roughly to the longitudes of India and Mexico) and two unstable points (at 165.3E and 14.7W, corresponding to longitudes of the Solomon Islands and the western edge of Africa), where the drift rate is negligible; but satellites not located at these points tend to shift in longitude away from the unstable toward the stable point over time. The stable points are where Earth's gravity has a local low, the unstable ones where it has a local high.

To stay in the intended position, geostationary satellites currently have to use thrusters to counteract these forces. Using thrusters means using up a limited resource -- fuel -- so stationkeeping is one thing that sharply limits a geostationary spacecraft's lifetime. To discuss fuel budgets, space navigators talk of "delta v," which is kind of a measure of how much change in velocity a spacecraft can accomplish, measured in units of speed. It takes about 50 meters per second of delta v per year to keep a geostationary satellite in Earth orbit, and almost all of that has to do with counteracting the tendency to tilt north and south in latitude rather than the tendency to drift east or west in longitude. The maximum delta v needed to counteract longitude drift for a satellite located right in between the stable and unstable points is about 2 meters per second. Since it's so small, the choice of longitude doesn't have a major effect on the lifetime of your geostationary satellite.

Silva and Romero show in their paper that the story is quite different at Mars, because Mars is much less spherical than Earth. It has a monstrous large pile of dense volcanic material deposited on one side (the Tharsis volcanoes and Olympus Mons), balanced on the opposite side by a broad gravity rise, that give its gravitational field much larger deviations from ideal smoothness than Earth has. Like at Earth, there are stable points over the two gravity lows and unstable points over the two gravity highs. Unlike at Earth, there is a huge cost if you want to put your satellite at a longitude between the stable and unstable points: Silva and Romero calculated that it can cost up to 22 meters per second of delta v per year in order to put a geostationary spacecraft at one of these spots. You would also have to perform stationkeeping maneuvers much more frequently at Mars than you do at Earth: approximately once every few days, rather than once every few weeks.

So where are the stable longitudes for Martian geostationary orbits? Totally by coincidence, they happen to be located at just about the same longitudes as they are on Earth, though their character is flipped. That is, the unstable points are at about the same longitudes as Earth's stable points, and vice versa. The stable longitudes at Mars are at 17.92W and 167.83E, and the unstable are 105.55W and 75.34E. (Note: the figure below has these points at slightly different locations. The map is based upon an analysis that didn't include a more detailed treatment of Mars' gravity field that Silva and Romero performed later in the paper.)

What does this mean for Martian communication satellites? You will probably have to put your satellite close to one of those four longitudes where the drift rate is low, to lengthen the potential lifetime of your mission. Where would that be with respect to our current missions -- would a spacecraft at one of those longitudes work as a communications satellite? Currently, we have landed missions located at 137.4E (Curiosity) and 6.0W (Opportunity).  Opportunity is relatively close to one of the stable longitudes; Curiosity is located in a relatively poor longitude.

One thing that works in our favor is that they're both located close to the equator; that would put any geostationary satellite in a very high position in the sky, and a position 30 degrees of longitude away from the satellite is actually no problem. The grid in the map below is a 30-degree one; you can see that Curiosity would be well-served by a geostationary satellite sitting at a longitude 30 degrees (or more) away from it.

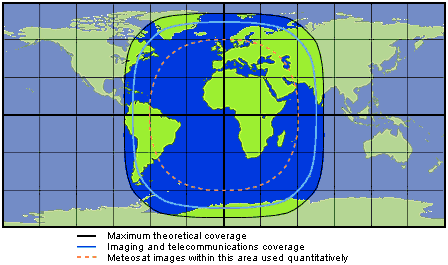
But one thing that works against us is that since Curiosity and Opportunity are located nearly on opposite sides of the planet, no one geostationary satellite could serve both spacecraft. And another problem, that I haven't even gotten into, is that it's costly in terms of delta v to get a spacecraft into such an orbit.

So don't expect to see a geostationary orbiter at Mars anytime soon. What has been proposed (but canceled) for Mars is a telecommunications orbiter that might circle at an intermediate altitude of around 5000 kilometers, giving it nice long communications passes over landers and a view of Earth that's only rarely obstructed by Mars.