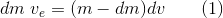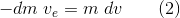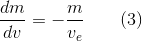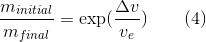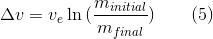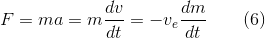Learn the rocket equation, part 1

One of the biggest barriers to exploring the solar system is that the rocket we use to launch a spacecraft on its journey must accelerate not only the payload, but all the propellant the rocket is about to use—or will ever use in the future. If we want the spacecraft to go faster, it’s intuitive that we need more propellant. But it turns out we need even more propellant than we think in order to accelerate the added propellant. This leads to exponential behavior—called the "rocket equation"—which puts tough limits on our ability to deliver large payloads to distant planets. In Part 1 of this article I’ll develop the basic concepts of the rocket equation, and in part 2 apply the concepts to a worked example: the New Horizons mission to Pluto.

To get started, let’s ask a fundamental physics question: what do rocket engines do? For our purposes the answer is: they consume propellant to produce energy, and they convert the resulting energy into force, which accelerates the rocket’s payload. In physics there are many ways to convert energy into force, so we need to be specific. For most of this discussion, I’ll use chemical rockets as the main example, though I’ll briefly mention other types in part 2. In a chemical rocket the propellant undergoes a chemical reaction that releases energy, and the rocket directs as much of that energy as possible into kinetic energy (energy of motion) of the ejected chemical product. Take NASA’s RS-25 engine as a specific example. It powered the Space Shuttle for three decades and is now being used in the Space Launch System. The RS-25 burns liquid hydrogen and liquid oxygen to release energy, and the resulting water molecules are ejected at high speed from the engine nozzle. The RL-10 engine, used in the Centaur second stage of the Atlas V launch vehicle, relies on the same chemistry. 

Now, remember Newton’s third law: for every action there is an equal and opposite reaction. It means the act of ejecting molecules pushes back on the rocket: every time a water molecule flies from the nozzle, the rocket loses a little mass and in return gains a little velocity. If the rocket burns fuel at a high rate, the reaction force on the rocket will be high, and so will the acceleration. The force is approximately proportional to the rate at which propellant is consumed.

Each type of chemical rocket has its own chemistry (liquid hydrogen and liquid oxygen; kerosene and liquid oxygen; solid fuel; etc.), and that chemistry combined with the design of the engine results in a characteristic velocity for the ejected molecules, called the exhaust velocity. (Technically it’s the “effective exhaust velocity,” but I’ll shorten it to “exhaust velocity” in an attempt at brevity. It’s also very closely related to the “specific impulse” which I won’t cover here but you can easily look up if you’re interested.) In the case of burning hydrogen, if all the energy released in the chemical reaction were perfectly and uniformly transferred into kinetic energy of the resulting water molecules, they would fly from the engine at about 5200 m/s. A real engine can’t achieve that velocity because some energy is inevitably lost to heat and light, and some of the molecules leave the engine traveling somewhat to the side, not straight backward, so the conversion of energy into velocity isn’t 100% efficient. The exhaust velocity for the RS-25 and RL-10 engines is about 4400 m/s in vacuum, 85% of the theoretical value.

Our goal is to figure out how the mass of propellant, the rocket, and the payload are related to the final velocity after the propellant is used up. We need a way to relate the change in mass to the change in velocity, and to do that we’ll use one of the most fundamental of all physical laws: the conservation of momentum. Momentum is simply the product of mass times velocity, and its direction matters, which means two momenta can cancel each other if they are pointed in opposite directions. In the figure below, in the left panel there is a rocket with total mass m at rest, with zero velocity and hence zero momentum. In the right panel, the rocket has ejected a small mass dm with velocity ve, the exhaust velocity, to the left, and as a result the rocket moves with a small velocity dv in the opposite direction, to the right.

Since momentum is zero in the left panel and is conserved, the total momentum in the right panel must also be zero, which means the leftward momentum of the ejected mass must equal the rightward momentum of the rocket:

If the ejected mass dm is very small compared with the total mass m, we should be able to ignore the –dm term on the right-hand side. However, if we do this, it’s important to be careful in the bookkeeping and encode in the equation the fact that a decrease in the mass of the rocket results in an increase in its velocity. A consistent convention is that both +dm and +dv should indicate increases in the mass and velocity of the rocket, which means reversing the sign of dm in Equation 1 (so that dm is now a negative number) and writing

The rocket ejects small masses molecule by molecule, each one adding a small increment to the rocket’s velocity and subtracting a bit from the remaining mass. Each time we can shift to a moving frame of reference where the rocket is stationary, as in the left panel of Figure 1, then apply the conservation of momentum. As time goes on, the rocket’s mass will drop as it consumes propellant. We want to know the cumulative effect of all the small velocity changes (all the dvs) during the rocket burn, relative to all the small mass changes (all the dms), and calculate a relationship between velocity and mass. First, rewrite Equation 2 as

It looks a little strange to write it this way, but what it says is the change in the rocket’s mass, per change in velocity, is proportional to the mass divided by the exhaust velocity. This is a direct consequence of the conservation of momentum and is true at every moment in time, even though the rocket’s mass and velocity are changing during the burn (I’ll assume the exhaust velocity remains constant). Now, if you’re familiar with differential equations and calculus, you may already know what to do with Equation 3: integrate it. If not, I must ask you to accept a mathematical leap of faith: it’s a well-established result that if the change in some quantity is proportional to the quantity itself, then the quantity varies exponentially. This sort of behavior occurs frequently in nature, including the exponential decay of radioactive isotopes and the exponential growth of bacteria when food is plentiful. In the present case the change in mass, with respect to change in velocity, is proportional to the mass itself, and therefore the rocket’s mass, as a function of velocity, obeys an exponential relation called the rocket equation. Written in a convenient form it looks like this:

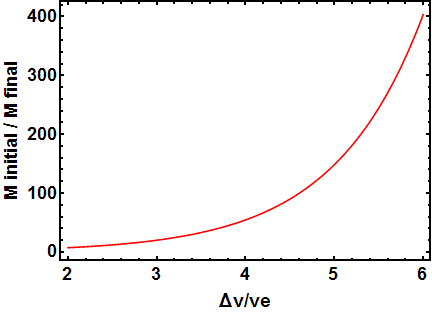
where the left-hand side is the ratio of the initial mass of the rocket (at the beginning of the burn) to the final mass (after the burn is complete), delta-v is the total change in velocity caused by the burn, and exp() is the exponential function. It’s a compact and beautiful result. In English it says the ratio of initial to final mass is the exponential of the ratio of delta-v to exhaust velocity, or, even more simply, the mass ratio is the exponential of the velocity ratio. The plot below shows Equation 4, where you can see how rapidly the mass ratio rises once the velocity ratio goes beyond 3 or 4; huge increases in mass are required for each increment of velocity. Often you’ll see the rocket equation written in an equivalent form, solved for delta-v: 

where ln() is the natural logarithm function, the inverse of the exponential function. 

You may have noticed that time appears nowhere in the rocket equation. That’s because the conservation of momentum “doesn’t care” how long it takes to use up propellant—the change in momentum, and therefore the final velocity, is the same. This is certainly true in the vacuum of empty space, far away from a planet. In the presence of gravity, though, it matters how fast a rocket consumes propellant. Imagine a rocket standing on the launch pad, burning its propellant so slowly that there’s not enough thrust to lift the rocket. All the propellant will be used up, and the rocket will go absolutely nowhere. This is an extreme example of an effect called gravity drag. The absolute amount of thrust is clearly important if our rocket is to leave the pad. If we divide both sides of Equation (2) by the small time interval dt during which the mass dm was ejected, and also make use of Newton’s famous second law of motion, force equals mass times acceleration, we get

where the acceleration a is the change in velocity per time, dv/dt. As before, note the minus sign: since dm/dt, the rate at which the rocket’s mass changes due to consuming propellant, is a negative number, the force is positive.

As a reward for the somewhat mathematical discussion above, we now have a quantitative answer to the original question, “What do rocket engines do?” They create force by burning propellant at some mass rate and ejecting the reaction product out the back of the engine at some exhaust velocity. The force, or thrust, of the engine is simply the exhaust velocity times the mass rate, and the final velocity ratio of the rocket is related to the mass ratio through either Equation (4) or (5). This basic toolbox allows us to calculate how much propellant we need to accelerate a rocket to the desired speed. In part 2 we’ll apply these tools to a practical example: launching a mission to Pluto.