David Shortt • Sep 27, 2013
Gravity assist
With the recent announcement by NASA that the 36 year-old spacecraft Voyager 1 has officially entered interstellar space at a distance from the Sun about four times further than Neptune's orbit, and with Voyager 2 not far behind, it seems worthwhile to explore how humans managed to fling objects so far into space.
Interplanetary spacecraft often use a maneuver called a gravity assist in order to reach their targets. Voyager 2 famously used gravity assists to visit Jupiter, Saturn, Uranus and Neptune in the late 1970s and 1980s. Cassini used two assists at Venus and one each at Earth and Jupiter in order to reach Saturn. New Horizons will arrive at Pluto in 2015 thanks to an assist at Jupiter. And Messenger used assists at Earth, Venus and three times at Mercury itself not to speed up, but to slow down enough to finally be captured by Mercury.

Mission planners use gravity assists because they allow the objective to be accomplished with much less fuel (and hence with a much smaller, cheaper rocket) than would otherwise be required. Lifting extra fuel into orbit, just so it can be used later, is exponentially expensive. Furthermore, the extra speed gained by gravity assists dramatically reduces the duration of a mission to the outer planets.
Gravity assists seem a bit mysterious, like one is getting something for nothing. This feeling can persist even if you know some physics. Since energy is conserved, you reason, how can a spacecraft obtain a net velocity boost by passing by a planet? Energy conservation suggests the spacecraft should speed up while approaching the planet, but then lose the same speed while departing. Recently I was talking with a colleague, an excellent plasma physicist who knew the phrase "gravity assist" but thought it must be marketing hyperbole because he didn't believe it could actually work. The mystery begs to be explained.
The key to understanding how a gravity assist works is to consider the problem from two different points of view, or reference frames. It's convenient to think about reference frames for both the planet and for the sun (or the solar system). For economy of language I'll call them the "planet frame" and the "sun frame."
In the planet frame, the planet sits still (by definition!). More importantly, since the planet is so much more massive than the spacecraft, the planet sits almost exactly at the center of mass of the two objects and does not react by any measurable amount as a result of the encounter. For example, Jupiter is about 10 to the 24th power times more massive than the Voyager spacecraft, so Jupiter ignores an encounter to an extremely high degree of precision. This means the spacecraft's total energy, made up of kinetic energy (energy of motion) plus potential energy (energy due to proximity to a massive object), is conserved throughout the encounter in this frame.
In the planet frame, then, the spacecraft indeed speeds up on approach and slows down by the same amount while departing, just like my colleague thought. During the approach, as the spacecraft falls into the gravity well of the planet, it gains kinetic energy (i.e. speed) and loses gravitational potential energy, trading one for the other just like a ball rolling downhill. After the encounter it climbs back out of the gravity well and loses whatever kinetic energy it gained during the approach, ending up with the same final speed it started with. The direction of the spacecraft changes during the encounter, however, so typically it leaves the planet heading in a different direction. The amount of deflection can be controlled by adjusting how close the spacecraft comes to the planet. The closer it gets, the greater the deflection. It's possible to have a very small deflection, near zero degrees, by arranging a wide miss. The maximum deflection is 180 degrees, sending the spacecraft back where it came from, obtained by arranging an extremely close approach. Mathematically the spacecraft's path is a hyperbola, so we say the spacecraft follows a hyperbolic trajectory in the planet frame.
Now let's consider what the encounter looks like in the Sun frame, where the Sun is stationary and the planet is moving. The difference between the planet frame and the Sun frame is just the velocity of the planet with respect to the Sun. To convert from the planet frame to the Sun frame, we simply add the velocity of the planet to both the planet and the spacecraft. This velocity is a vector, which means direction is important, and it can be in any arbitrary direction depending on the planet's position in its orbit at the time of the encounter (It also changes with time because the planet is following a curved orbit around the sun, but during the relatively short encounter with the spacecraft it's a reasonable approximation to consider the planet as moving in a straight line). Because the direction of the spacecraft changes when it encounters the planet and because the original direction of the spacecraft is also arbitrary, it's not immediately obvious how the encounter will look in the Sun frame. The arbitrariness of the directions gives rise to a rich set of possible behavior in the Sun frame, all in accordance with Newton's laws of motion, even though in the planet frame the encounters are simple hyperbolic trajectories. Crucially, because the direction changes, the speed of the spacecraft is different before and after the encounter when viewed in the Sun frame. The outgoing speed is not the same as the incoming speed, and the spacecraft can either speed up or slow down. Let's see by example how this works.
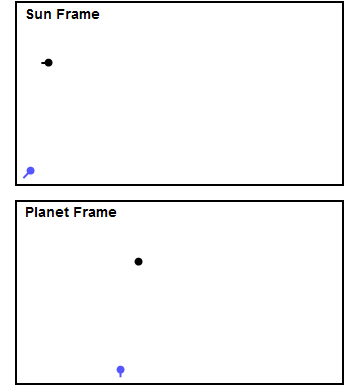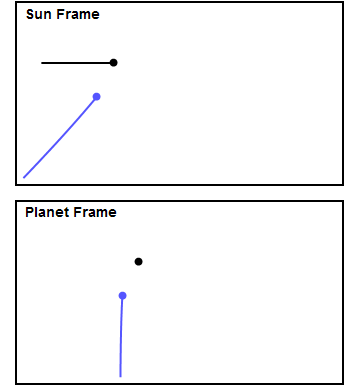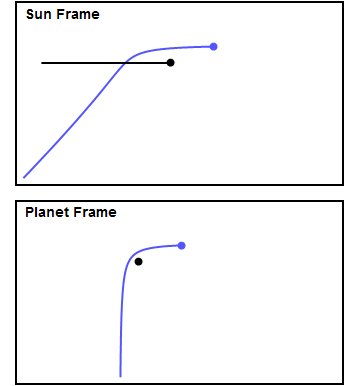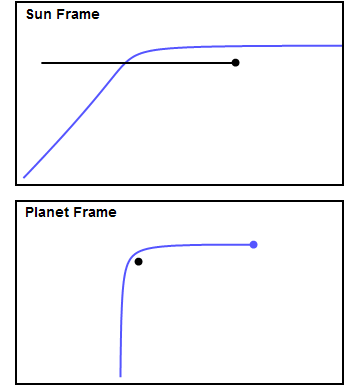
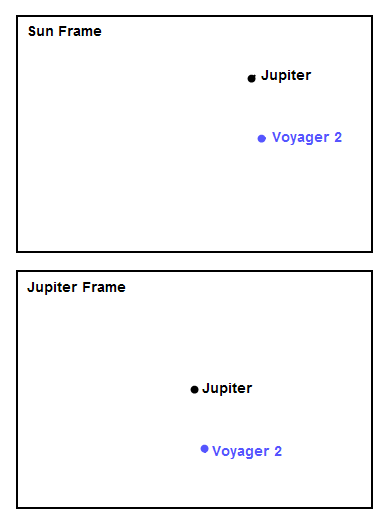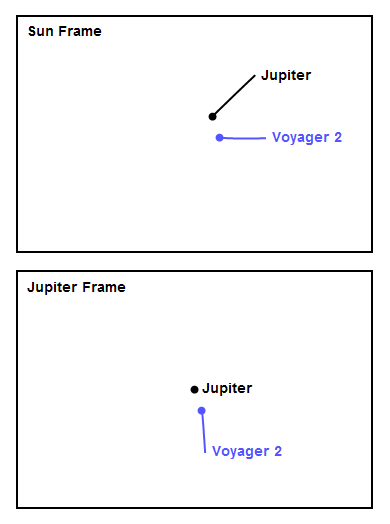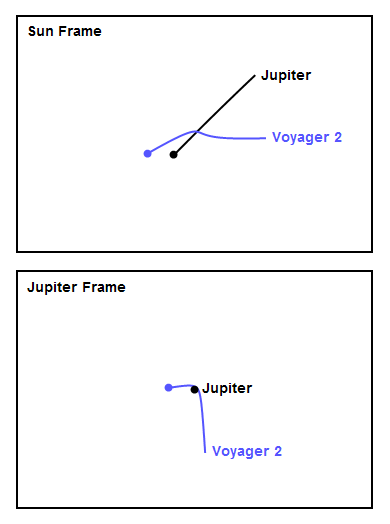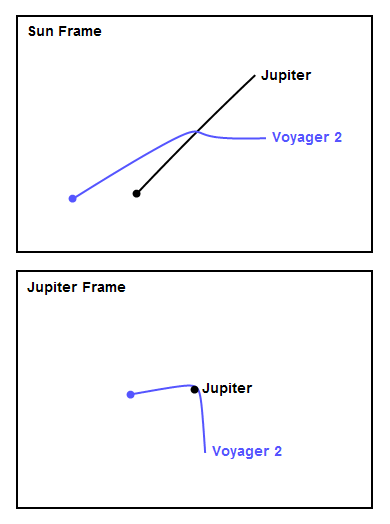
Figure 1 shows a made-up example of an encounter. The top panel shows the encounter in the Sun frame, in which the planet (in black) is moving to the right, and the spacecraft (in blue) experiences a gravity assist. The bottom panel shows the view from the planet frame, in which the spacecraft approaches the planet from below and the planet sits still. I chose the approach parameters so that the trajectory is bent through approximately 90 degrees in the planet frame. In the planet frame the spacecraft leaves the planet with the same speed with which it approached, but in the Sun frame it's clear the spacecraft gains quite a bit of speed. You can see how the spacecraft approaches the planet from behind, accelerates as it gets closer, and "slingshots" around the planet. In this example the spacecraft gains about 60% of the planet's own velocity. We'll see later on that this example is fairly close to what happened to Voyager 2 at Jupiter, Saturn and Uranus.
How does this happen? Consider that in the bottom panel the spacecraft initially moves vertically with some velocity, call it v. After the encounter it leaves the planet with the same velocity v, but in the horizontal direction. To convert to the sun frame, we add the planet's velocity (which I chose arbitrarily to be v in the horizontal direction) to both the planet and the spacecraft. Using the Pythagorean Theorem, in the Sun frame the spacecraft initially has a total velocity equal to the square root of the sum of the squares of the vertical and horizontal velocities, that is v times the square root of 2, or about 1.4v. It leaves the planet with v + v = 2v in the horizontal direction, having gained about 0.6v, or about 60% of the planet's velocity. This shows clearly why the velocity of the spacecraft in the Sun frame increases during the encounter - it's because the spacecraft's direction of motion changes to point along the planet's direction.
This is a general rule of thumb for gravity assists: if, after the encounter, the spacecraft is pointing more along the planet's direction than it was before the encounter, its speed will increase. But where does the energy come from to accelerate the spacecraft? In fact it comes from the planet's own energy of motion. In the Sun frame, there is a transfer of momentum and kinetic energy from the planet to the spacecraft. The planet slows down very slightly in its orbit, and the spacecraft speeds up. Newton's third law states, "To every action there is an equal and opposite reaction," and that's true in this case. Because the planet is so much more massive than the spacecraft, the transfer doesn't affect the planet to any measurable extent, but to the spacecraft it's a big deal. For example, we can calculate that during the Voyager encounters with Jupiter in 1979, Jupiter slowed down by roughly 10 to the -24th power kilometers per second -- a change much too small to measure. But each Voyager gained about 10 km/s, a pretty big number and enough to put them on a fast path to Saturn (and in the case of Voyager 2, to Uranus and Neptune as well) and eventual escape from the solar system.
Depending on the relative direction of motion of the planet and the spacecraft, a gravity assist can either speed up, slow down, or merely change the direction of the spacecraft. Figure 2 shows a gallery of possibilities. The center panel (e) shows the view in the planet frame, and the other panels show the sun frame with 8 different directions for the planet's motion. The trajectories in panels (a), (b) and (d) slow down the spacecraft, those in panels (f), (h) and (i) speed it up, and those in panels (c) and (g) change the direction but not the speed. Panel (f) is the same example we considered in Figure 1. It's worth emphasizing that every panel depicts a correct solution of Newton's laws, so any of these could be arranged by a mission designer if needed.
Before looking at a real mission, let's recap what we know so far. In the planet frame, the trajectory is hyperbolic with the same velocity before and after the encounter but with the path deflected through some angle. In the Sun frame this results in trajectories that can speed up or slow down the spacecraft in addition to changing its direction, depending on the geometry of the encounter. Total energy is conserved, and the planet loses (or gains) an insignificant but real amount of velocity, while the spacecraft's velocity and direction may change by a large amount.
Next let's consider a practical example. Voyager 2 is a good choice because it used gravity assists to visit all four of the outer planets: Jupiter, Saturn, Uranus and Neptune. (Voyager 1 followed a similar trajectory up to Saturn, but then had to leave the plane of the solar system and forgo any more planets because mission planners arranged the encounter to include a close approach of Saturn's large and fascinating moon Titan. Voyager 2 did not have a Titan encounter and went on to visit Uranus and Neptune.)
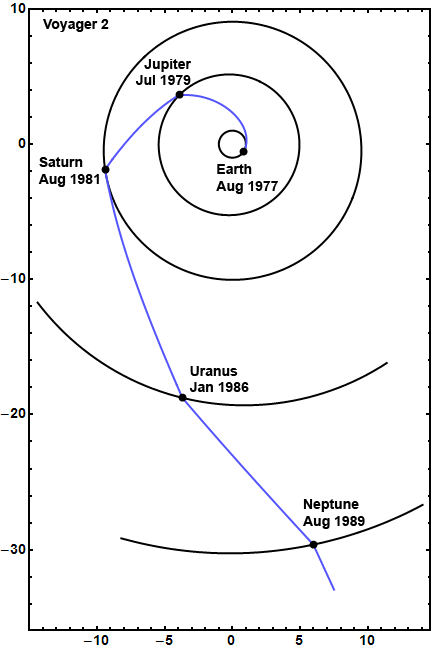
Figure 3 shows a plot of the path of Voyager 2 from its launch from Earth in 1977 through its encounter with Neptune 12 years later. For simplicity the plot omits the orbits of Mercury, Venus and Mars. The axes are labeled in astronomical units, or AU, with the sun at the center (1 AU is the average distance between the Earth and the sun). Notice the particularly sharp "left turns" Voyager 2 makes at Jupiter and Saturn. Viewed as a whole, though, the path of Voyager 2 is a reasonably smooth spiral from Earth to Neptune. This is no accident. The outer planets line up in such a fortuitous way about every 175 years, and it encourages the idea of using gravity assists repeatedly to direct the spacecraft to the next target.
Figures 4-7 show close-up animations of the encounters at the four outer planets in both the Sun frame and the planet frame. For all the figures, the frame rate is 1 frame per day, the trajectories are shown for 20 days before and after the moment of closest approach, and all the figures are shown at the same spatial scale for comparison, with a width of about 0.6 AU. The Jupiter encounter in Figure 4 looks a lot like panel (i) in Figure 2. You can see how unusual the Jupiter encounter looks in the Sun frame, with the spacecraft experiencing a "bump" in its trajectory as it first accelerated toward massive Jupiter, then whipped around behind it. At Saturn, the encounter in Figure 5 looks a lot like panel (f) in Figure 2. Notice the high speed of the encounter - Voyager was moving fast due to the speed it gained at Jupiter, and the approach had to be very close in order to execute the screaming left turn needed to reach Uranus. The modest left turn at Uranus, shown in Figure 6, looks tame by comparison. Finally, at Neptune in Figure 7, Voyager 2 actually turned slightly right, thereby losing some speed. The reason is that mission planners wanted to arrange a close flyby of Neptune's large moon Triton, and this necessitated flying mostly over Neptune's north pole and making a slight right turn in addition to plunging down, out of the plane of the solar system (the plunge down is not visible in Figure 7 since it's a view from overhead).
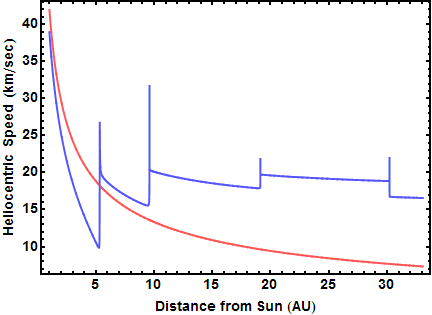
Another insight from the animations is that Voyager 2's speed increased quite a bit during its journey. Figure 8 confirms this by plotting the spacecraft's speed in the sun frame (in blue) vs. its distance from the sun in AU. Also plotted, in red, is the escape velocity from the sun, i.e. the speed necessary at that distance to ensure escape from the solar system. After leaving Earth but before its encounter with Jupiter, Voyager 2 lacked enough speed to escape the sun's gravity (the blue curve lies below the red curve between 1 AU and 5 AU). During the Jupiter encounter, Voyager 2 gained enough speed to enable it to leave the solar system - the blue curve stays above the red curve beyond Jupiter. It gained about 10 km/s at Jupiter, about 5 km/s at Saturn, about 2 km/s at Uranus, and lost about 2 km/s at Neptune. As of September 2013, Voyager 2 is over 102 AU from the sun and still traveling at about 15 km/s. Due to its slightly different trajectory, Voyager 1 is over 125 AU from the sun and traveling about 17 km/s, and NASA recently announced that Voyager 1 has officially entered interstellar space.
Thanks to gravity assists, the Voyagers are headed to the stars.
Let’s Go Beyond The Horizon
Every success in space exploration is the result of the community of space enthusiasts, like you, who believe it is important. You can help usher in the next great era of space exploration with your gift today.
Donate Today

 Explore Worlds
Explore Worlds Find Life
Find Life Defend Earth
Defend Earth