Figuring out orbital positions from orbital elements

A few times a year I find myself confronting a table full of numbers describing the orbits of things in the solar system, and cursing at myself because I've forgotten, again, what all these numbers mean and how to manipulate them to get the particular numbers I want. In particular, despite the fact that determining perihelion and aphelion distances from semimajor axis length and eccentricity could hardly be easier, I still always draw a blank. So I'm sitting down now to write a blog entry that will tell me what these numbers mean and how to use them to get the numbers I want! I'm posting it because I figure it'll be useful for some of you, too. In the following post, I'll show you why I was interested in getting these numbers today.

Here we go. The shape of an elliptical orbit is described by two parameters:

• semi-major axis, a: one half of the ellipse's long axis
• eccentricity, e: 0 for circular orbits; between 0 and 1 for ellipses

To compute other numbers describing the shape of the orbit, here's what you do:

• Periapsis distance = a(1-e)
• Apoapsis distance = a(1+e)
• Orbital period = 2π√(a³/GM)
• Orbital period (solar orbit, in years, with a in AU) = a^1.5
  (and recall that 1 AU = 149.60×10⁶ km)

To figure out where an object currently is in space requires a few more pieces of information, including inclination, longitude of ascending node, et cetera.

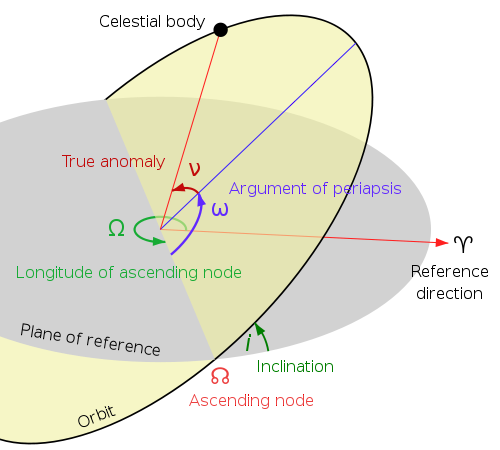
But because of the particular way in which orbital parameters are usually reported, it's actually quite difficult to use these elements to determine a body's current position in space in a way that makes intuitive geometrical sense to me. (I'm a geologist, dangit, not an orbital mechanic!) It's much faster and easier to make JPL's HORIZONS system crunch the numbers. (It makes me feel slightly better that when I asked this question on Twitter, all three Kuiper belt astronomers who follow me said they use HORIZONS too.) You can use HORIZONS via a telnet or email interface but if you don't have too many things to calculate it's easiest just to use the web interface. So:

• Go to http://ssd.jpl.nasa.gov/horizons.cgi
• Change the Target Body to the one you're interested in (click "change" and search on the name or number or provisional designation)
• Change Observer Location to "@sun"
• Go to Table Settings and check "Helio eclip. lon & lat" (or set the list to "18,20" to get heliocentric lat/lon and range)
• Click Generate Ephemeris and look for "hEcl-Lon" and "hEcl-Lat," which are in degrees, and "delta," which is the range in AU.

Note: It defaults to a one-month time span with a time step of one day, so the output table will have about thirty entries in it, starting today. The time span permits you to choose a wide range of dates (for most Kuiper belt objects, I find it to cover 1600 to 2200), and the time step chooser permits you to pick calendar years and calendar months as well as increments of days, hours, minutes, or seconds.

HORIZONS can also be used to find the distance between Earth and any of these objects, too, obviously; and you can have it spit the results directly to a text file, which is very handy!