The edge of "round": Three half-megameter moons

Posted by Emily Lakdawalla

2010/08/18 05:28 CDT

Topics:

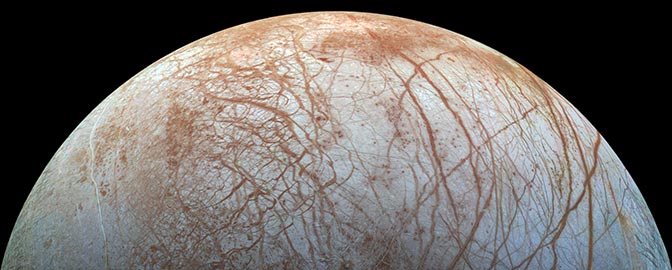
Part of the definition of a planet is a solar system body's roundness. Big things in the solar system are round, because their self-gravity is strong enough to overcome the inherent strength of the materials that they're made of. It helps that big things also tend to be relatively warm, with heat left over from their formation and from the decay of radioactive elements; warm substances are not as strong as cold substances, especially if conditions are warm enough to turn solids into interior liquids or even gases. Thus the perfectly roundest looking bodies in the solar system are the giant planets and Venus. Smaller, colder bodies, with puny self-gravity, can't overcome the strength of their hard rock and ice components to pull themselves together, and stay lumpy.

Of course, the solar system is not made of just round things and just lumpy things; it's a continuum. Any time you try to sort continuously varying things into sharply defined categories, you run in to trouble with the stuff at the borders. In the outer solar system, where bodies incorporate a lot of ice, the boundary between "round" and "lumpy" seems to fall at a diameter of roughly 500 kilometers. Here are a few things that lie on that edge between "round" and "not round."

NASA / JPL / SSI / processing by Gordan Ugarkovic (Enceladus, Mimas) and Ted Stryk (Miranda)

Three half-megameter moons

Large objects in the solar system are round; small objects are lumpy. Where does round transition to lumpy? In the outer solar system, the transition happens at roughly 500 kilometers, give or take. Enceladus (512 kilometers) is geologically active and very round, while Miranda (472 kilometers) and Mimas (397 kilometers) have noticeable departures from roundness.

None of these bodies is a candidate for being called a "planet," because they're all moons. The IAU did briefly flirt with the definition of "planet" being independent of whether a body happened to orbit another planet, or the Sun, and it is interesting to wonder where the planetary geophysicists would have drawn the line among these three moons. Would Enceladus qualify for inclusion in the "like a planet" club? It seems that all the moons in the outer solar system that are larger than Enceladus would -- although, interestingly, the next largest moon after Enceladus is Tethys, which (at 1,066 kilometers) has more than double Enceladus' diameter.

You may have noticed that I specified that this diameter appears to be a boundary only in the outer solar system. Closer to the Sun, in the asteroid belt, where things are much more rocky and much less icy, the rules may be different. With a diameter that averages 529 kilometers but which ranges from 458 to 578, Vesta is slightly larger than Enceladus, yet definitely not "round." Ceres (at 960 kilometers) definitely is round though. And again we have that gap in size, with no bodies having diameters between half and one megameter. I'm not arguing that that's anything more than a coincidence -- but it's a curious one!

Ben Zellner, Peter Thomas, and NASA

3-D model of Vesta

This simulated view of the second most massive asteroid, Vesta, was created from a topographic model developed from two dozen images caotured by the Hubble Space Telescope in 1995. The most astonishing feature of the model was an impact crater at the south pole (bottom of this image), with a width 80 percent the width of Vesta itself.