Emily Lakdawalla • May 13, 2008
Landing ellipses
This morning there was a press conference on the upcoming landing of Phoenix, so you will probably be seeing many articles on Phoenix in the mainstream news media. Sadly, I failed to notice how early the press conference was (8 am my time) so I missed it -- I'll try to catch it again if it gets replayed on NASA TV. This conference is usually just an overview of what the mission is designed to do, what events to expect on landing day (May 25), and a reminder of the mixed previous success record for Mars landings. Here's a direct link to the press kit (PDF format, 3 MB), a 47-page document about the mission that contains a lot of basic overview as well as more detail about the science goals, mission hardware, and mission timeline.
One thing I have mentioned several times already, and which I will be mentioning again through next week, is the Phoenix "landing ellipse." What's a landing ellipse? A short definition is that it's the area on Mars in which the spacecraft is likely to land. But that only begs more questions: why don't they know precisely where it's going to land, and why is the possible landing area elliptical rather than circular or any other shape? For a more detailed explanation I turned to Rob Manning, who was in charge of the Mars Exploration Rover landing and who is now working on figuring out how and where the Mars Science Laboratory rover will make it safely to the surface. I asked him to tell me about what the landing ellipse signifies, and also to talk about "1-sigma" and "3-sigma" ellipses, terms you often see when you read more technical documents about landing sites.
NASA / JPL-Caltech / Washington Univ. St. Louis / JHU APL / Univ. of Arizona
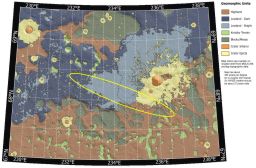
The Phoenix landing ellipse
Phoenix is scheduled to land May 25, 2008 in a region above Mars' Arctic Circle. Its landing ellipse (the region in which there is a 99.9% certainty that the lander will come to rest) is about 100 kilometers long and 19 kilometers wide, centered at approximately 68 degrees North, 234 degrees East. The ellipse has been shifted downrange by about 13 kilometers from an earlier, similar map in order to avoid boulder-rich regions that are now just off the northwestern end of the ellipse.The landing team has very detailed models for all of these variables -- the spacecraft, its entry point, the properties of the atmosphere, and so on. "When you put all of these together and simulate (in the months before landing) the whole process, from Mars approach through touchdown, instead of a single touch-down point on the surface, you get a whole ton of points (where each point is the result of a single landing day computer simulation) that are centered on our "target" landing site latitude and longitude." That is to say, they run their model many times, and let the values for these variables fluctuate within their expected parameters, and on each run the model spits out a latitude and longitude for the actual point of landing.
Rob continued, "The 'scatter' of possible landing points is denser in the middle and sparser and sparser as you get further from the center. This scatter is approximately shaped like a cigar [that is, an ellipse] that is aligned from the northwest (the direction that Phoenix is coming from) across the 'green valley' to the southeast. The result is that the probability of landing in the "middle most" square kilometer (at the target center) is higher than [the probability of landing in] a square kilometer that is far to the northwest of the center."
The possible landing points are normally distributed, which means that they follow a bell curve, with the probability being higher in the center of the ellipse and lower as you get farther from the center. Rob said, "In this case it is a two-dimensional distribution, in that it covers an area over the surface of Mars and not just a single line. Like all statistics, this distribution has a mean (the middle of the ellipse) and a standard deviation (two, actually, one for each direction). In engineer-speak we call the length of one standard deviation, 'one sigma'" or 1σ.
"For Phoenix, the distribution that we expect TODAY (it might get bigger or smaller as we get closer to Mars over the next week or so) has one sigma being about 17 kilometers long in the long axis of the cigar and about three kilometers long in the short axis of the ellipse. You can then draw an ellipse that 'covers' one standard deviation (one sigma) on the surface of Mars. That ellipse is (17 x 2) kilometers long and (3 x 2) kilometers wide, because a standard deviation is like a radius -- it is measured out from the center of the ellipse.
"The probability that Phoenix will land inside that 1-sigma ellipse happens to be only 39%. In order to find a shape on the surface that has a high probability of containing the true landing site, we typically choose three standard deviations for our landing ellipse or '3-sigma'. Our 3-sigma ellipse is centered on our target point (like the 1-sigma ellipse) and is also oriented in the same direction. However, it is three times bigger, (17 x 2 x 3 or about 100) kilometers long by (3 x 2 x 3, about 20) kilometers wide. The probability that Phoenix will land inside its 3-sigma ellipse is 98.8%. Very high.
"The odds of Phoenix landing outside this ellipse is then 1-0.988 = 1.2%. This makes the 3-sigma ellipse a safe bet for those who care about where it lands (as we do!)."
"For the math fans out there, the probability that Phoenix will land inside "k" standard deviations (or k-sigma) is exactly:
"So when you see a Mars landing ellipse, you now know that the center of that ellipse is much more likely than near its edges! Now we simply have to get ready, set, aim!
"(so far so good!)"
Thanks very much to Rob for the detailed explanation!
Let’s Go Beyond The Horizon
Every success in space exploration is the result of the community of space enthusiasts, like you, who believe it is important. You can help usher in the next great era of space exploration with your gift today.
Donate Today

 Explore Worlds
Explore Worlds Find Life
Find Life Defend Earth
Defend Earth