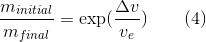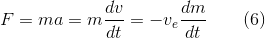Learn the rocket equation, part 2

In Part 1 of this article, we looked at the physics of rockets and the rocket equation:

or

in which the mass ratio (the ratio of initial to final mass of the rocket) is related to the velocity ratio (the ratio of the delta-v achieved by the rocket, to the exhaust velocity ve). (For consistency, I’ll keep the same numbering scheme for equations and figures as in Part 1.) In this Part 2, we’ll explore what the rocket equation has to say about travel through the solar system using the example of launching a rocket to Pluto.

What can we conclude about the rocket equation? Is it good for us or bad for us? Unfortunately for planetary exploration, when we plug in real numbers it tends to be bad for us. The velocity needed to escape Earth’s gravity and reach other planets in a short time is on the order of 15 km/s or more, four or five times greater than the exhaust velocities generated by typical chemical rockets which are in the range 3–4 km/s. A glance at this figure from Part 1 of this article tells us a velocity ratio of 5 requires the initial mass of the rocket to be many times greater than the final mass, more than a factor of 100. Unfortunately, this violates all the rules of good science and engineering—we have no way to build a rocket where 99% of the total mass is propellant and only 1% is used for the tanks, engine, fairing (to protect the payload during launch) and other inert mass, and not forgetting the payload itself. That’s the bad news: the chemistry of rockets, combined with the depth of Earth’s gravity well and the very large distance to other planets, conspire against us. As they say, “Space is hard.”

A classic approach to get around this problem is to use multi-stage rockets. Once the first-stage propellant is exhausted, we jettison the tanks, engine and other inert mass and start again with the second stage. From the point of view of each stage, the “payload” it needs to accelerate is all the remaining stages, plus the actual payload. The rocket equation applies to each stage individually, and the sum of the delta-vs for all the stages is the final delta-v of the payload. For example, if we built a 3-stage rocket where each stage had a mass ratio of 5 and an exhaust velocity of 3 km/s, then Equation 5 from part 1 says each stage would give a delta-v of about 4.8 km/s, and the final delta-v would be about 14.5 km/s. That’s in the ballpark of what we need to reach deep space. However, as we’ll see shortly, this approach results in a very small payload mass relative to the initial mass at launch. 

To see how the rocket equation works in a practical example, let’s consider the New Horizons mission to Pluto. New Horizons was launched on January 19, 2006. As it departed earth, it had a velocity of about 17 km/s and passed the orbit of the moon in only 8.5 hours. The spacecraft lost speed as it climbed out of the Earth’s gravity well, then the Sun’s, performed a gravity assist at Jupiter in February 2007 to gain about 4 km/s, lost speed again as it climbed away from the Sun toward Pluto, and zoomed past Pluto at about 13 km/s on July 14, 2015, about 9.5 years after launch. Let’s apply the rocket equation during the launch phase and see how New Horizons achieved the necessary delta-v. In what follows I relied on published specifications for the various components of the system but made many approximations and omitted some details in the interest of brevity. I trust purists will forgive the simplifications. In the end the results have an error less than 10%, a pretty good payoff for the effort.

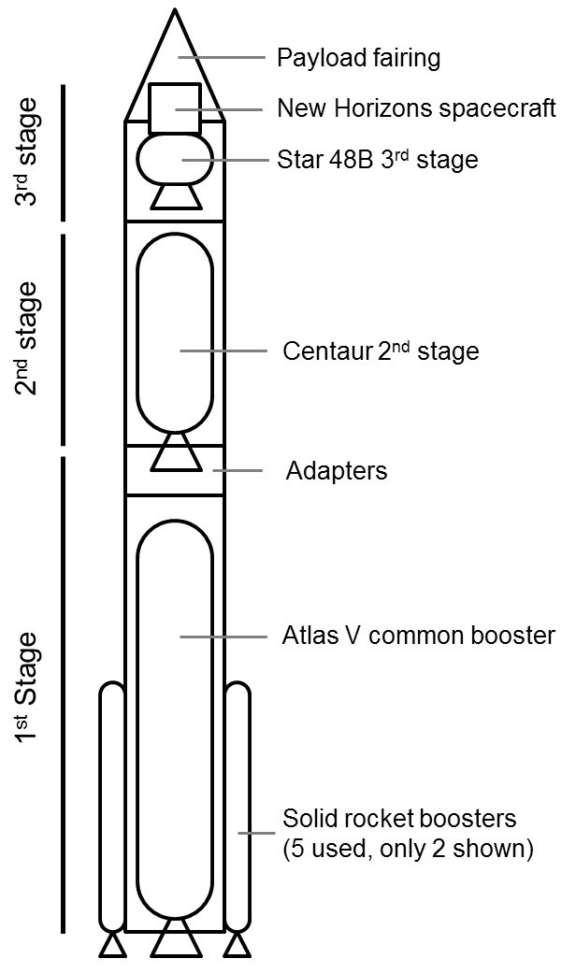
New Horizons used a reliable launch system, the Atlas V manufactured by United Launch Alliance (ULA), with five solid rocket boosters (SRBs) and an added Star 48B third stage manufactured by Orbital ATK. A simplified diagram is shown in the figure below, followed by a table of parameters adapted from ULA and Orbital ATK literature. Simplifications include assuming a constant average burn rate and exhaust velocity for each stage; rounding masses and exhaust velocities; combining some inert mass items together; and ignoring gravity drag and air resistance.

Next, let’s break the launch into four steps and apply the rocket equation to each one: (1) the time from launch until the solid rocket boosters (SRBs) are exhausted, about 95 seconds; (2) the remaining booster phase until the common booster is exhausted; (3) the Centaur second stage, assumed here to occur in a single burn; (4) the Star 48B third stage. During step 1 it’s necessary to use a weighted-average exhaust velocity in the rocket equation because both the common booster and the SRBs are firing simultaneously. The correct weighting factors are the respective burn rates. The table below shows the result of the rocket-equation analysis. For each step, the initial and final masses are obtained by adding up the appropriate pieces from the table above. Then the mass ratio and exhaust velocity go into the rocket equation (Equation 5 from Part 1) to get the delta-v for that step. In between steps, inert mass is jettisoned, so the initial mass for the next step is less than the final mass from the previous step. (I should note here one additional simplification: this analysis jettisons the fairing along with the booster at the end of step 2, while in reality the fairing was jettisoned somewhat earlier, during the booster burn.)

The final delta-v is the sum of the delta-vs from each step: 18.2 km/s. Considering all the simplifications, this result is reasonably accurate. The value actually achieved was 16.8 km/s, about 8% lower. The biggest reason for the difference is an effect called gravity drag, which I mentioned in Part 1 but have not accounted for in this simple model. The early phase of the launch, in the vertical direction, is inefficient because the engine’s thrust must counter the pull of gravity or else the rocket will go nowhere. As a result the rocket’s acceleration, and hence its eventual delta-v, is reduced by the strength of gravity. This would not be the case if the rocket were launched horizontally on an imaginary frictionless railway, for example—on such a track the rocket would accelerate even with low thrust. To minimize the effects of gravity drag, the rocket pitches over as soon as possible to follow a path more closely parallel to the Earth’s surface and gain horizontal speed. The propellant used during the early vertical phase is necessary to lift the rocket above most of the atmosphere so it can gain speed later without burning up, but that propellant is mostly wasted from the point of view of delta-v. The actual delta-v is therefore somewhat less than we calculate from the rocket equation. Another drag effect I have ignored is air resistance, which is important but not as large as gravity drag.

The multi-stage approach allowed NASA to accelerate New Horizons to a high enough velocity to reach Pluto, but at a price: the ratio of payload mass (478 kg) to total launch mass (about 570,000 kg) is less than 0.1%. The precious spacecraft made up less than one part in a thousand of the launch mass! And the total science payload (spectrograph, cameras, etc.) was only about 30 kg, about 0.005% of the launch mass. Getting a small instrument package to Pluto in less than a decade required pretty much everything that today’s science and technology could deliver. NASA used one of the largest rockets available, the Atlas V, added five solid rocket boosters, added a third stage, and used a small payload. The designers threw everything they had at the problem and were able to deliver 30 kg of science instruments to Pluto in 9.5 years. It’s sobering to comprehend how immensely difficult it is to travel across the solar system, and what an inspiring accomplishment it is to make such a journey even with the smallest payload.

Having gone to all the trouble to send a spacecraft to Pluto, you might ask, why didn’t NASA design New Horizons to stop at Pluto and go into orbit, like Cassini did at Saturn or Juno did at Jupiter, providing a much better opportunity to study the Pluto-Charon system close-up over many years, rather than a few days during a flyby? New Horizons approached Pluto at about 13 km/s. Orbital velocity depends on the radius of the orbit, of course, but a reasonable value for Pluto is on the order of 0.5 km/s, much less than New Horizons’ approach speed. To slow down, New Horizons would need to carry with it enough propellant to reduce its speed by more than 12 km/s in order to be captured into orbit. We can explore this possibility with the rocket-equation toolbox, which can be used either to accelerate or decelerate.

A glance at the delta-vs in the last table above shows just how difficult it would be to slow down at Pluto. Even the combination of the Centaur and Star 48B is not quite enough to do the job, giving a total delta-v of only about 11 km/s. But suppose, just for the sake of discussion, that it was enough. The problem then is that it would be necessary to deliver the entire Centaur plus the Star 48B (or some equivalent deceleration system), plus the spacecraft to Pluto—a total of about 28,000 kg. To do that in the same 9.5 years requires the Atlas booster and SRBs to provide a huge delta-v, about 18 km/s in the model above. But the Atlas and five SRBs together only give about 7 km/s. Hypothetically doubling the number of SRBs to ten would only nudge the delta-v up to 7.5 km/s, still not nearly enough. The point is, the Atlas V could not provide a high enough delta-v to that much mass, and so it was not possible for New Horizons to reach Pluto with enough remaining propellant to slow down and enter orbit. It was all NASA could do to get it there; stopping was out of the question.

What other options do we have to move around the solar system at will? Equation 5 says that increasing the mass ratio will increase the delta-v supplied to the payload, so one approach is to build beefier multi-stage rockets like the Space Launch System (SLS). NASA estimates that future versions of the SLS will be powerful enough to launch an orbiter to Uranus or even a sample-return mission to Enceladus. Unfortunately the natural logarithm function ln() in Equation 5 increases slowly, so bigger rockets yield diminishing returns.

Equation 5 also says that increasing exhaust velocity boosts delta-v. Ion engines like the ones used in the Dawn spacecraft have exhaust velocities in the neighborhood of 30,000 m/s, ten times higher than chemical rockets, and they can use solar panels to obtain energy from the sun. The downside of ion engines is that the absolute value of the thrust is small, about 0.09 Newtons (0.3 ounces) in the case of Dawn’s engines. Such small thrust is not enough for launch, but once the spacecraft is in space, the ion thrust can be applied for months or years at a time, accelerating or decelerating a 1000-kg spacecraft by kilometers per second using modest amounts of propellant. Ion-engine technology allowed Dawn to stop at and orbit two different solar system bodies, Vesta and Ceres, the first time such a feat has been accomplished.

Other high-exhaust-velocity technologies have been, or are being developed. A few examples are nuclear thermal engines, which use nuclear energy rather than chemical energy to heat an inert propellant to high temperature and expel it from the engine; VASIMR (Variable Specific Impulse Magnetoplasma Rocket) engines, which use radio waves and magnetic fields to ionize and accelerate an inert gas plasma; and Hall thrusters, another form of ion thruster which ionizes and accelerates a plasma with a DC electric field.

A more radical alternative is not to carry any propellant at all, but instead to use purely external energy to accelerate the spacecraft. Solar sailing is one example, where the small pressure of sunlight, applied over a large sail area for a long time, provides enough force to change the spacecraft’s velocity by meaningful amounts. Readers may know the Planetary Society is actively exploring this technique with the LightSail spacecraft. The Breakthrough Starshot initiative is another novel approach which aims to employ a powerful ground-based laser to transmit energy to a sail and accelerate a very lightweight spacecraft fast enough, roughly 10% of the speed of light, to reach a nearby star within a human lifetime.

Time will tell if nuclear energy, the power of light, or some other innovative technology can be used to move spacecraft around the solar system, or beyond, on a large scale. For the near future, chemical rockets will continue to do the heavy lifting, constrained by the rocket equation and working hard to push spacecraft out of Earth’s gravity well and through interplanetary space.