Darin Ragozzine • Oct 17, 2016
Rapidly Rotating Regular Satellites and Tides
As we begin the 2016 Division for Planetary Sciences (DPS) meeting, I’d like to provide a hypothesis to explain a surprising result from the 2015 DPS meeting. We were all excited and awed to see the new results from NASA’s New Horizons mission and its Pluto flyby. As an orbital dynamicist, perhaps the most striking piece of news was the unusual rotation rates and states of Pluto’s small moons.
I agreed with Emily Lakdawalla’s assessment that the revelation of rapid rotation at right angles was the most interesting result. Quietly, in a later session, my student Danielle Hastings (then at Florida Tech, now a graduate student at UCLA) presented results that Hi’iaka, the outer satellite of Haumea – another dwarf planet – was also rapidly rotating. Is there a connection?
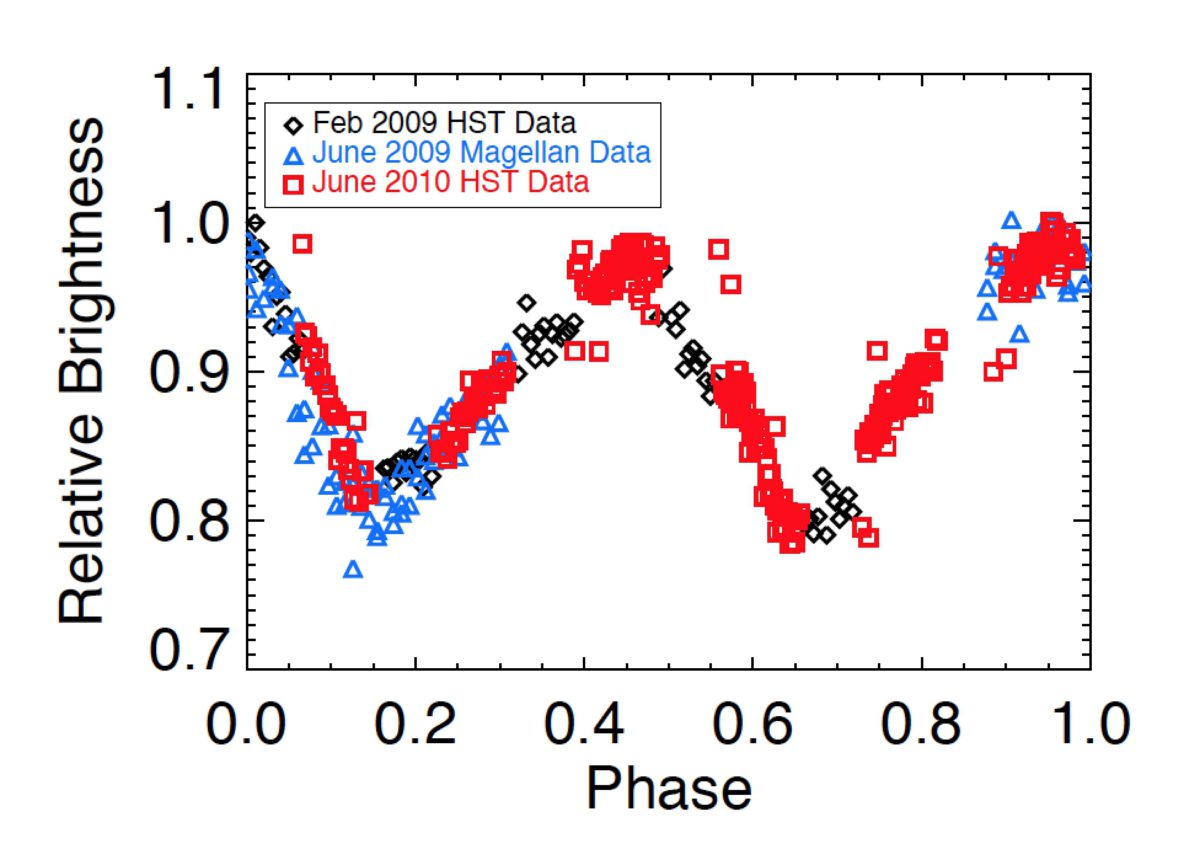
Well, life and teaching and moving to new institutions happened, but Danielle and I are happy to report that the paper presenting our Hi’iaka results has been accepted and posted to arXiv. We solidify our understanding of Hi’iaka’s 10-hour spin rate (compared to the 50-day orbital period) and then conjectured that Hi’iaka, like Pluto’s moons, has a spin axis misaligned with its orbit. Depending on the degree of misalignment (called the obliquity), changes to Hi’iaka’s spin-induced light curve are probably already detectable. (I recently received funding for an “archival” Hubble Space Telescope proposal that will investigate this in more detail.)
Since our presentation last year, we have done a lot of work to try to understand how Hi’iaka could be rapidly rotating despite the fact that it is on a “normal” nearly circular orbit. All the most recent journal articles about Haumea admit that its formation – including the formation of its moons – is still unclear with no hypothesis matching all the data. Still, formation through some kind of collision is most likely. There are reasons to doubt this hypothesis, but let’s explore the standard outcome of a collision which is the formation of a disk of material very close to Haumea. In the classic moon formation story, this material would eventually coalesce into 1-2 moons. Then, over the age of the solar system, tidal forces and torques can change the spin and orbital properties.
In the same way, our own Moon is thought to have been mostly formed at a distance of ~3 Earth radii (any closer and Earth tides rip a forming Moon back apart). Tides are then invoked to move it to its current position at ~60 Earth radii. Tides that move moons out are very slow; it is only because of the incredible precision of lunar laser ranging that we can directly detect the present-day growth of the Moon’s orbit by 4 cm/year. The other side of the lunar-orbit-expansion coin is the slowing of Earth’s spin by 2 milliseconds per century; these effects are coupled by conservation of energy and angular momentum.
In the standard tidal picture, this process of “tidal despinning” is very slow for the more massive planet, but very fast for the small moon. This matched our observations that the major moons of Earth, Mars, Jupiter, Saturn, Uranus, and Neptune were all “tidally despun,” i.e., rotating at the same rate as their orbit, always keeping the same face of the moon towards the planet. Exceptions were explainable: Saturn’s moon Hyperion has a chaotic (meaning unpredictable) rotation rate due to its aspherical shape and eccentric orbit. The tiny and distant irregular satellites are so far out and so small that tides aren’t expected to affect them. And so on.
The moons of Pluto and Haumea don’t fit nicely into this story. They are relatively large and relatively close to their planet, making them “regular” satellites. They show evidence for significant tidal expansion of the semi-major axis, which is supposed to be FAR slower than the time needed to despin the satellites. And yet they appear to be almost untouched by the most powerful tidal despinning effect.
Well, tides are extremely fickle. Every time I think I can pin them down, they seem to wriggle free. To understand why, let’s recall why tides affect orbits at all. The tidal (or differential gravitational) force that a body experiences can easily be time-variable due to rotation or eccentric orbits. This creates a situation where materials are subjected to a repetitive squishing and stretching motion. Since real planets and moons are made of real materials, these squishing and stretching motions are influenced by friction, turning orbital energy into heat. For us orbital dynamicists, used to measuring precise and well-behaved orbits, the complex geophysical response of real materials with all their imperfections adds a messiness that makes clear conclusions difficult. Furthermore, it takes billions of years of tides (that are certainly changing in unpredictable ways) to lead to significant orbital changes. As a result, dynamicists are used to admitting that our understanding of how tides really work in real systems could be off by a factor of 10-1000! It would not be unusual to say that tides would have effect X over a timeframe of 0.1-100 million years… maybe.
So, one explanation for the rapidly rotating satellites is simply to say that, for these objects, tides are 1000 (or more!) times weaker than we see elsewhere, so they aren’t significantly affected by tides and can retain their original rotation rates (set by collisions in the moon-forming disk). This is certainly within the realm of possibility, but this oversimplifies the result.
Despite the uncertainties associated with tides, there is one dynamical fact that helps us: tides are extremely sensitive to distance. All else being equal, changing the planet-moon distance by a factor of 2 changes the strength of tides by a factor of 2*2*2*2*2*2=64 (or so). That means that Earth’s moon, which used to be ~30 times closer to the Earth, had tides that were almost a billion times stronger. Suddenly, even factor of 1000 uncertainties in the geophysics of tides become unimportant and we’re back to being able to estimate the effect of tides.
Hi’iaka and Pluto’s moons must have been so strongly affected by tides when they were close, that the general feeling is that these objects would have almost immediately tidally despun. If you crunch the numbers, you find that it might take, at longest, ~1000 years to despin Hi’iaka when it was close to Haumea. Compared to the age of the solar system, this is so short that the standard story would say that Hi’iaka ~instantly despins. Then, as the story goes, as Hi’iaka’s orbit expands, it’s orbital period gets longer (by Kepler’s Third Law) but this only requires a tiny correction to the spin in order to keep the spin and orbital period locked (“synchronous”). Therefore, all regular satellites are tidally despun to synchronous.
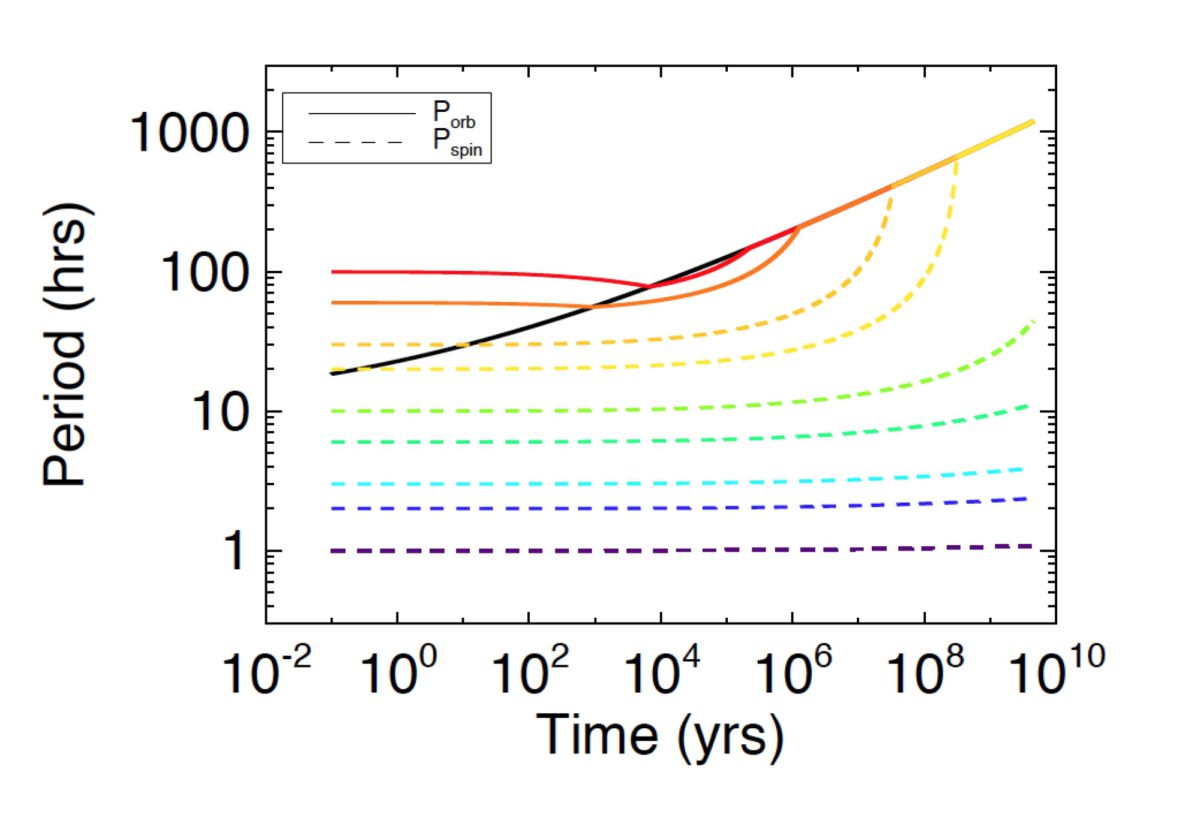
The problem is that tidal despinning and orbital expansion are happening at the same time. If the despinning timescale changes from 100 years to 1000 years due to semi-major axis expansion that happens in only 50 years, then synchroneity is not an inevitable outcome. We found that numerical calculations (very approximate given our extremely limited understanding of tides) were required to say whether satellites really could or should despin in the age of the solar system (see the figure below).
In the case of Hi’iaka, it seems like the semi-major axis expansion was so fast that the despinning tides just couldn’t keep up. With reasonable tidal parameters, you can easily keep Hi’iaka rotating rapidly given almost any starting conditions. So, we hypothesize that despinning tides on Hi’iaka were only strong for a very short time, allowing Hi’iaka’s present-day rapid rotation. (It’s worth noting we explore several other hypotheses trying to explain Hi’iaka’s spin and find that they don’t work except in very contrived circumstances.)
What about Pluto’s moons? Does the same answer work for them? Possibly. Pluto’s moon system is very different because of the very massive Charon (large enough to arguably call Pluto-Charon a “double planet” and to say that the other moons are orbiting both bodies). As with Haumea, the formation of the small moons of Pluto is unclear, but their locations near resonances and at relatively large distances from Pluto seem to indicate that they were pushed to their current locations by Charon’s tidal expansion. (Larger moons tidally expand more rapidly and tidally despin more rapidly.) If so, then the same underlying reasoning can explain what happened to the spins of the small moons of Pluto: riding Charon’s very fast tidal expansion, their orbits grew so fast their despinning tides couldn’t keep up. Even though our paper was about Hi’iaka, we did a quick check to see if our hypothesis can also explain Pluto’s moons and the story seems to work.
The Pluto and Haumea systems are really in a different regime of tides than any other object in the solar system because they have strong tides and dynamically interacting moons. Earth and Mars have strong tides but only one moon (Earth) or moons that are too small to dynamically interact (Mars). The gas and ice giant satellite systems have very interactive moons, but since gaseous atmospheres don’t mind getting stretched and squished, tides are 100-1000 times weaker. Hence, the “unusual” spin rates of moons around Pluto and Haumea can be partially attributed to their unique tidal circumstances (rapid expansion and/or dynamically interacting moons).
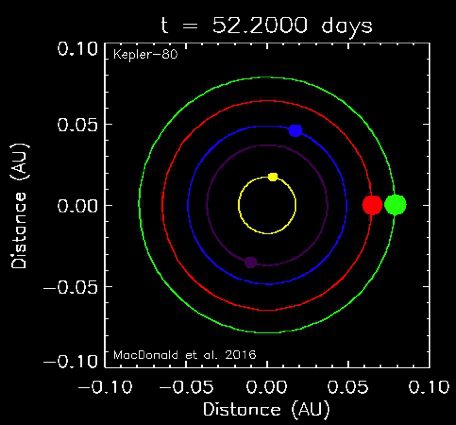
While we hope that we can study more such systems in our solar system, another step forward in understanding tides in multi-body systems may come from exoplanets. Another student (Mariah MacDonald, now a Penn State grad student) and I recently completed a detailed dynamical analysis of a 5-planet system called Kepler-80. Although stars have weak tides like gas giants, these planets orbit very closely (all 5 between 0.02 and 0.08 AU), so tides should be important. A simulation (by Daniel Fabrycky at University of Chicago) shows that tidal effects can naturally put this system into a configuration where the outer four planets have uniquely synchronized orbits that exactly match the observed orbital configuration. [Note that we have essentially no information on the spin rates of any exoplanets.] This gives us additional insight into how tides work in multi-body systems.
Studying tides in more specific ways for the hundreds of multiple exoplanet systemsmay teach us how tides work in these systems. Combined with improved analyses of planets and moons in the solar system may allow for future DPS meetings where researchers pin down tides well enough to get specific answers. In the meantime, we’ll have to settle for more qualitative answers and see whether our hypothesis for the rapid rotation of these dwarf planet moons holds up to future scrutiny.
Let’s Go Beyond The Horizon
Every success in space exploration is the result of the community of space enthusiasts, like you, who believe it is important. You can help usher in the next great era of space exploration with your gift today.
Donate Today

 Explore Worlds
Explore Worlds Find Life
Find Life Defend Earth
Defend Earth